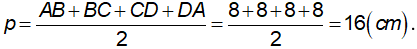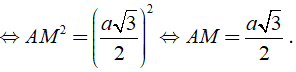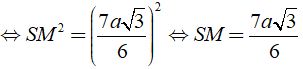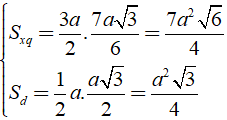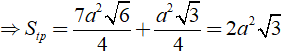A. Lý thuyết
1. Công thức diện tích của hình chóp đều
a) Diện tích xung quanh của hình chop đều
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn:
Sxq = p.d (p: nửa chu vi đáy, d: trung đoạn)
b) Diện tích toàn phần của hình chóp
Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy:
Stp = Sxq + S (S: diện tích đáy)
2. Công thức thể tích của hình chóp đều
Thể tích của hình chóp bằng một phần ba của diện tích đáy nhân với chiều cao:
V = 1/3S.h (S: diện tích đáy, h: chiều cao)
3. Ví dụ áp dụng
Ví dụ: Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, cạnh đáy là 8cm, chiều cao 10cm.
+ Tính diện tích xung quanh và diện tích toàn phần của hình chóp.
+ Tính thể tích của hình chóp.
Hướng dẫn:
Ta có ABCD là hình vuông, khi đó nửa chu vi bằng:
+ BD = AC = √ (82 + 82) = 8√ 2 ( cm ) ⇒ AO = BO = CO = DO = 4√ 2 ( cm )
Do đó:
+ Diện tích xung quanh của hình chóp đều là Sxq = p.d = p.OB = 16.4√ 2 = 64√ 2 ( cm2 ).
+ Diện tích toàn phần của hình chóp đều là
Stp = Sxq + SABCD = 64√ 2 + 82 = 64 + 64√ 2 ( cm2 )
+ Thể tích của hình chóp đều là V = 1/3S.h = 1/3.SABCD.SO = 1/3.82.10 = 640/3( cm3 )
B. Bài tập
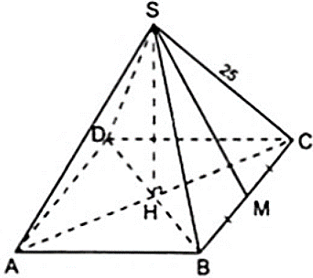
Bài 1: Một hình chóp đều có độ dài cạnh bên là 25cm, đáy là hình vuông ABCD có cạnh bằng 30cm. Tính diện tích toàn phần của hình chóp.
Hướng dẫn:
Gọi M là trung điểm của BC thì SM là đường cao của mặt bên SBC (vì tam giác SBC cân tại S)
Áp dụng công thức: Stp = Sxq + Sd
Ta có: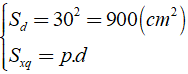
Áp dụng định lí Py – ta – go vào tam giác SCM vuông tại M
SC2 = CM2 + SM2 ⇒ 252 = 152 + SM2 ⇔ SM2 = 202 ⇔ SM = 20( cm )
Do đó: Sxq = 60.20 = 1200( cm2 ) ⇒ Stp = 1200 + 900 = 2100( cm2 )
Bài 2: Tính diện tích toàn phần của hình chóp tam giác đều có cạnh đáy bằng a và chiều cao bằng 2a.
Hướng dẫn:
Xét hình chóp S.ABC có AB = AC = BC = a và SH = 2a.
Gọi M là trung điểm của BC thì AM vừa là đường trung tuyến, vừa là đường cao, vừa là đường phân giác của tam giác đều ABC nên AM ⊥ BC và HM = 1/3AM.
Áp dụng định lý Py – ta – go vào tam giác vuông ABM vuông tại M ta được:
AB2 = BM2 + AM2 ⇒ a2 = ( a/2 )2 + AM2
Do đó HM = (a√3) /6.
Áp dụng định lí Py – ta – go vào tam giác vuông SHM vuông tại H, ta có:
SM2 = HM2 + SH2 ⇒ SM2 = ( (a√3) /6 )2 + ( 2a )2
Áp dụng công thức: Stp = Sxq + Sd
Ta có:
Thông báo: Blog Lương Điệp (luongdiep.com) là nơi chia sẻ Template Powerpoint; Trò chơi Powerpoint; Tài liệu Giáo dục; Bài giảng điện tử; Giáo án điện tử; Đề thi: học tập trực tuyến, ... miễn phí, phi lợi nhuận.
Nếu bạn sở hữu file do bản quyền thuộc về bạn, hãy liên hệ ngay với chúng tôi để chúng tôi tháo gỡ theo yêu cầu. Xin cám ơn!