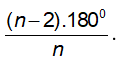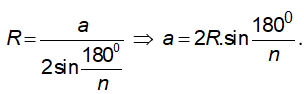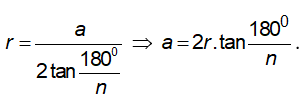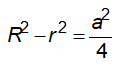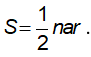1. Định nghĩa
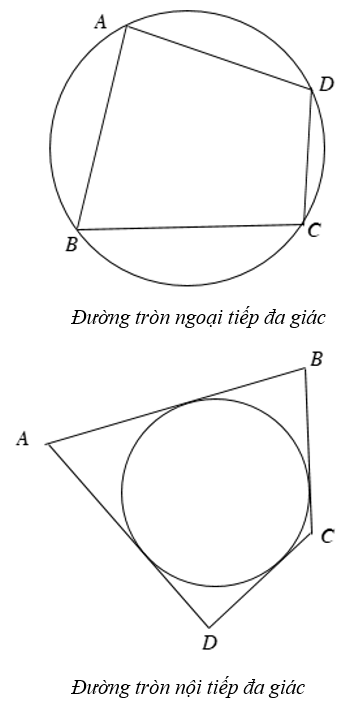
+ Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác được gọi là đa giác nội tiếp đường tròn.
+ Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp đa giác và đa giác được gọi là đa giác ngoại tiếp đường tròn.
2. Định lý
+ Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.
+ Tâm của hai đường tròn này trùng nhau và được gọi là tâm của đa giác đều.
+ Tâm này là giao điểm hai đường trung trực của hai cạnh hoặc là hai đường phân giác của hai góc.
3. Mở rộng
+ Bán kính đường tròn ngoại tiếp đa giác là khoảng cách từ tâm đến đỉnh.
+ Bán kính đường tròn nội tiếp đa giác là khoảng cách từ tâm O đến 1 cạnh.
+ Cho n_ giác đều cạnh a. Khi đó:
– Chu vi của đa giác: 2p = na (p là nửa chu vi).
– Mỗi góc ở đỉnh của đa giác có số đo bằng
– Mỗi góc ở tâm của đa giác có số đo bằng 360°/n.
– Bán kính đường tròn ngoại tiếp:
– Bán kính đường tròn nội tiếp:
– Liên hệ giữa bán kính đường tròn ngoại tiếp và nội tiếp:
– Diện tích đa giác đều:
4. Ví dụ cụ thể
Câu 1: Một đường tròn có bán kính R = 3cm. Tính diện tích hình vuông nội tiếp đường tròn đó.
Hướng dẫn:
Ta có: Bán kính đường tròn ngoại tiếp:
Do tứ giác nội tiếp là hình vuông với n = 4, khi đó: a = R√2 = 3√2.
Diện tích hình vuông là: S = a2 = (3√2)2 = 18 cm2.
Thông báo: Blog Lương Điệp (luongdiep.com) là nơi chia sẻ Template Powerpoint; Trò chơi Powerpoint; Tài liệu Giáo dục; Bài giảng điện tử; Giáo án điện tử; Đề thi: học tập trực tuyến, ... miễn phí, phi lợi nhuận.
Nếu bạn sở hữu file do bản quyền thuộc về bạn, hãy liên hệ ngay với chúng tôi để chúng tôi tháo gỡ theo yêu cầu. Xin cám ơn!