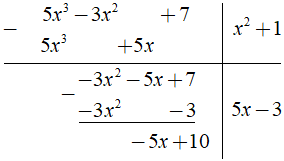1. Phương pháp
Ta trình bày phép chia tương tự như cách chia các số tự nhiên. Với hai đa thức A và B của một biến, B≠0 tồn tại duy nhất hai đa thức Q và R sao cho:
A = B.Q + R, với R=0 hoặc bậc của R nhỏ hơn bậc của B.
Nếu R=0, ta được phép chia hết.
Nếu R≠0, ta được phép chia có dư.
Ví dụ: Sắp xếp các đa thức theo lũy thừa giảm dần của biến rồi làm phép chia:
a, ( x3 – 7x + 3 – x2 ) : ( x – 3 ).
b, ( 5x3 + 7 – 3x2 ) : ( x2 + 1 ).
Hướng dẫn:
a) Ta có:
Khi đó ta có: ( x3 – 7x + 3 – x2 ) = ( x – 3 ).( x2 + 2x – 1 )
b) Ta có
Khi đó ta có ( 5x3 + 7 – 3x2 ) = ( x2 + 1 )( 5x – 3 ) – 5x + 10.
Thông báo: Blog Lương Điệp (luongdiep.com) là nơi chia sẻ Template Powerpoint; Trò chơi Powerpoint; Tài liệu Giáo dục; Bài giảng điện tử; Giáo án điện tử; Đề thi: học tập trực tuyến, ... miễn phí, phi lợi nhuận.
Nếu bạn sở hữu file do bản quyền thuộc về bạn, hãy liên hệ ngay với chúng tôi để chúng tôi tháo gỡ theo yêu cầu. Xin cám ơn!