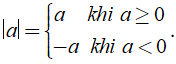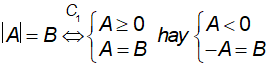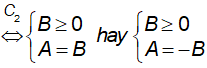Bài 5: Phương trình chứa dấu giá trị tuyệt đối

A. Lý thuyết

1. Nhắc lại về giá trị tuyệt đối

Giá trị tuyệt đối của số a, được kí hiệu là | a |, ta định nghĩa như sau:

Ví dụ: Bỏ dấu giá trị tuyệt đối và rút gọn biểu thức sau:

a) A = | x – 1 | + 3 – x khi x ≥ 1.

b) B = 3x – 1 + | – 2x | khi x < 0.

Hướng dẫn:

a) Khi x ≥ 1 ta có x – 1 ≥ 0 nên | x – 1 | = x – 1

Do đó A = | x – 1 | + 3 – x = x – 1 + 3 – x = 2.

b) Khi x < 0 ta có – 2x > 0 nên | – 2x | = – 2x

Do đó B = 3x – 1 + | – 2x | = 3x – 1 – 2x = x – 1.

2. Giải một số phương trình chứa dấu giá trị tuyệt đối

a) Phương pháp chung

Bước 1: Áp dụng định nghĩa giá trị tuyệt đối để loại bỏ dấu giá trị tuyệt đối

Bước 2: Giải các bất phương trình không có dấu giá trị tuyệt đối

Bước 3: Chọn nghiệm thích hợp trong từng trường hợp đang xét

Bước 4: Kết luận nghiệm

b) Một số dạng cơ bản

Dạng

hoặc

Dạng | A | = | B | ⇔ A = B hay A = – B.

Dạng phương trình có chứa nhiều dấu giá trị tuyệt đối

+ Xét dấu các biểu thức chứa ẩn nằm trong dấu GTTĐ.

+ Chia trục số thành nhiều khoảng sao cho trong mỗi khoảng, các biểu thức nói trên có dấu xác định.

+ Xét từng khoảng, khử các dấu GTTĐ, rồi giải PT tương ứng trong trường hợp đó.

+ Kết hợp các trường hợp đã xét, suy ra số nghiệm của PT đã cho.

Ví dụ: Giải bất phương trình | 4x | = 3x + 1

Hướng dẫn:

Ta có | 4x | = 3x + 1

+ Với x ≥ 0 ta có | 4x | = 4x

Khi đó phương trình trở thành 4x = 3x + 1

⇔ 4x – 3x = 1 ⇔ x = 1.

Giá trị x = 1 thỏa mãn điều kiện x ≥ 0, nên 1 là một nghiệm của phương trình đã cho

+ Với x < 0 ta có | 4x | = – 4x

Khi đó phương trình trở thành – 4x = 3x + 1

⇔ – 4x – 3x = 1 ⇔ – 4x = 1 ⇔ x = – 1/7.

Giá trị x = – 1/7 thỏa mãn điều kiện x < 0, nên – 1/7 là một nghiệm cần tìm.

Vậy phương trình đã cho có tập nghiệm là S = { – 1/7;1 }

B. Bài tập

Bài 1: Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau:

a) A = 3x + 2 + | 5x | với x > 0.

b) A = | 4x | – 2x + 12 với x < 0.

c) A = | x – 4 | – x + 1 với x < 4

Hướng dẫn:

a) Với x > 0 ⇒ | 5x | = 5x

Khi đó ta có: A = 3x + 2 + | 5x | = 3x + 2 + 5x = 8x + 2

Vậy A = 8x + 2.

b) Ta có: x < 0 ⇒ | 4x | = – 4x

Khi đó ta có: A = | 4x | – 2x + 12 = – 4x – 2x + 12 = 12 – 6x

Vậy A = 12 – 6x.

c) Ta có: x < 4 ⇒ | x – 4 | = 4 – x

Khi đó ta có: A = | x – 4 | – x + 1 = 4 – x – x + 1 = 5 – 2x.

Vậy A = 5 – 2x

Bài 2: Giải các phương trình sau:

a) | 2x | = x – 6

b) | – 5x | – 16 = 3x

c) | 4x | = 2x + 12

d) | x + 3 | = 3x – 1

Hướng dẫn:

a) Ta có: | 2x | = x – 6

+ Với x ≥ 0, phương trình tương đương: 2x = x – 6 ⇔ x = – 6.

Không thỏa mãn điều kiện x ≥ 0.

+ Với x < 0, phương trình tương đương: – 2x = x – 6 ⇔ – 3x = – 6 ⇔ x = 2.

Không thỏa mãn điều kiện x < 0.

Vậy phương trình đã cho vô nghiệm.

b) Ta có: | – 5x | – 16 = 3x

+ Với x ≥ 0, phương trình tương đương: 5x – 16 = 3x ⇔ 2x = 16 ⇔ x = 8

Thỏa mãn điều kiện x ≥ 0

+ Với x < 0, phương trình tương đương: – 5x – 16 = 3x ⇔ 8x = – 16 ⇔ x = – 2

Thỏa mãn điều kiện x < 0

Vậy phương trình đã cho có tập nghiệm là S = { – 2;8 }

c) Ta có: | 4x | = 2x + 12

+ Với x ≥ 0, phương trình tương đương: 4x = 2x + 12 ⇔ 2x = 12 ⇔ x = 6

Thỏa mãn điều kiện x ≥ 0

+ Với x < 0, phương trình tương đương: – 4x = 2x + 12 ⇔ – 6x = 12 ⇔ x = – 2

Thỏa mãn điều kiện x < 0

Vậy phương trình đã cho có tập nghiệm là S = { – 2;6 }

d) Ta có: | x + 3 | = 3x – 1

+ Với x ≥ – 3, phương trình tương đương: x + 3 = 3x + 1 ⇔ – 2x = – 2 ⇔ x = 1.

Thỏa mãn điều kiện x ≥ – 3

+ Với x < – 3, phương trình tương đương: – x – 3 = 3x + 1 ⇔ – 4x = 4 ⇔ x = – 1

Không thỏa mã điều kiện x < – 3

Vậy phương trình đã cho có tập nghiệm là S = { 1 }