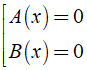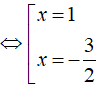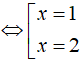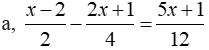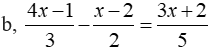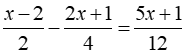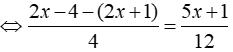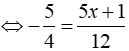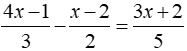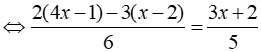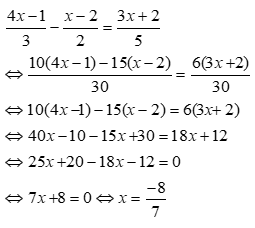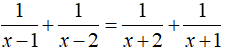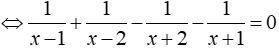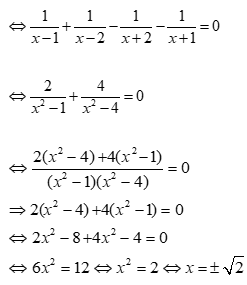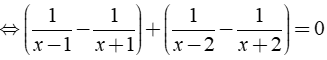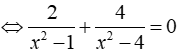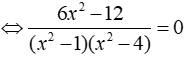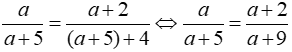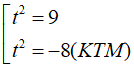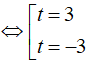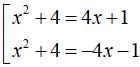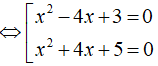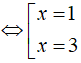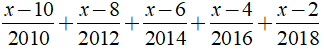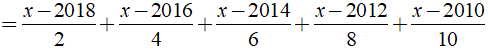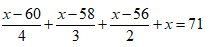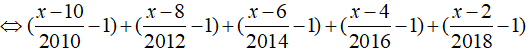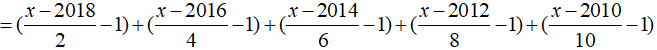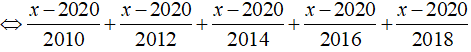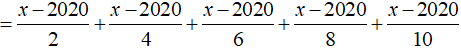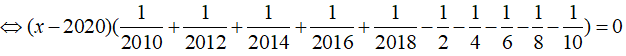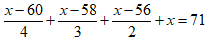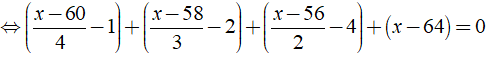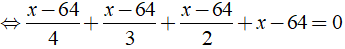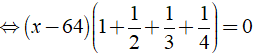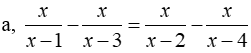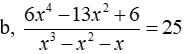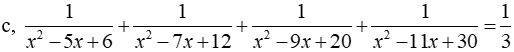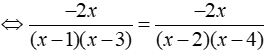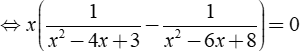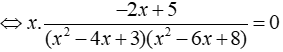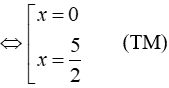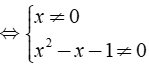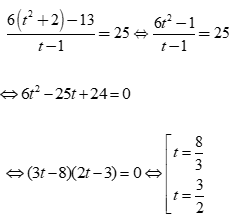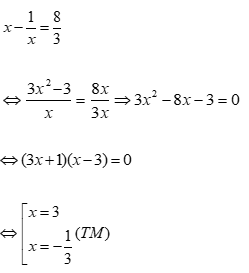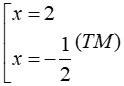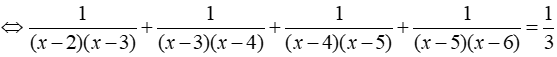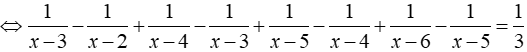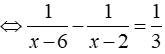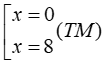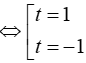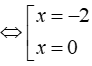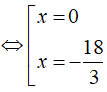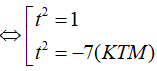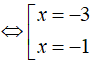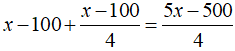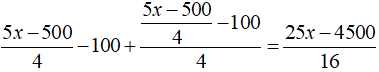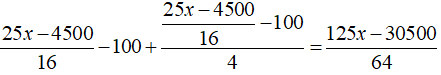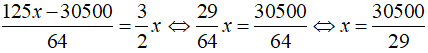A. Lý thuyết
1. Định nghĩa về phương trình một ẩn
+ Một phương trình với ẩn x là hệ thức có dạng A( x ) = B( x ), trong đó A( x ) gọi là vế trái, B( x ) gọi là vế phải.
+ Nghiệm của phương trình là giá trị của ẩn x thoả mãn (hay nghiệm đúng) phương trình.
2. Định nghĩa về phương trình bậc nhất một ẩn
Phương trình có dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn.
3. Các quy tắc biến đổi phương trình
a) Quy tắc chuyển vế
Trong một phương trình ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.
b) Quy tắc nhân với một số
Trong một phương trình, ta có thể nhân cả hai vế với cùng một số khác 0.
4. Cách giải phương trình bâc nhất một ẩn
Cách giải:
Bước 1: Chuyển vế ax = – b.
Bước 2: Chia hia vế cho a ta được: x = – b/a.
Bước 3: Kết luận nghiệm: S = – b/a .
Ta có thể trình bày ngắn gọn như sau:
ax + b = 0 ⇔ ax = – b ⇔ x = – b/a.
Vậy phương trình có tập nghiệm là S = – b/a .
5. Cách giải đưa về phương trình ax + b = 0
Để giải các phương trình đưa được về ax + b = 0 ta thường biến đổi phương trình như sau:
Bước 1: Quy đồng mẫu hai vế và khử mẫu (nếu có)
Bước 2: Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax = c.
Bước 3: Tìm x
Chú ý: Quá trình biến đổi phương trình về dạng ax = c có thể dẫn đến trường hợp đặc biệt là hệ số của ẩn bằng 0 nếu:
0x = c thì phương trình vô nghiệm S = { Ø } .
0x = 0 thì phương trình nghiệm đúng với mọi x hay vô số nghiệm S = R.
6. Phương trình tích và cách giải
Phương trình tích có dạng A( x ).B( x ) = 0
Cách giải phương trình tích A( x ).B( x ) = 0 ⇔
Cách bước giải phương trình tích
Bước 1: Đưa phương trình đã cho về dạng tổng quát A( x ).B( x ) = 0 bằng cách:
Chuyển tất cả các hạng tử của phương trình về vế trái. Khi đó vế phải bằng 0.
Phân tích đa thức ở vế phải thành nhân tử
Bước 2: Giải phương trình và kết luận
7. Phương trình chứa ẩn ở mẫu
a) Điều kiện xác định
Điều kiện xác định của phương trình là tập hợp các giá trị của ẩn làm cho tất cả các mẫu trong phương trình đều khác 0.
Điều kiện xác định của phương trình viết tắt là ĐKXĐ.
b) Cách giải
Ta thường qua các bước:
Bước 1: Tìm điều kiện xác của phương trình
Bước 2: Quy đồng mẫu hai vế rồi khử mẫu.
Bước 3: Giải phương trình tìm được.
Bước 4: Kết luận.
8. Cách giải bài toán bằng cách lập phương trình
Các bước giải toán bằng cách lập phương trình:
Bước 1: Lập phương trình
+ Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
+ Biểu diễn các đại lượng chưa biết khác theo ẩn và các đại lượng đã biết.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Trả lời
Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
B. Bài tập
1. Nhận biết – Thông hiểu
Bài 1: Phương trình (1) và (2) có tương đương hay không?
(1) x – 1 = 4
(2) (x – 1)x = 4x
Hướng dẫn:
Phương trình (1) x – 1 = 4 có tập nghiệm S1 = 5
Phương trình (2): (x – 1)x = 4x ⇔ (x – 1)x – 4x = 0 ⇔ (x – 5)x = 0
Phương trình (2) có tập nghiệm là S2 = 0;5
Vì S1 ≠ S2 nên hai phương trình (1) và (2) không tương đương.
Bài 2: Tìm điều kiện của m để phương trình sau là phương trình bậc nhất một ẩn:
a) (2m – 1)x + 3 – m = 0
b) (3m – 5)x + 1 – m = 0
Hướng dẫn:
a, (2m – 1)x + 3 – m = 0 là phương trình bậc nhất một ẩn
⇔ 2m – 1 ≠ 0
⇔ m ≠ 1/2
b, Tương tự phần a ta được: m ≠ 5/3
Bài 3: Cho phương trình 2(x + 3) – 3 = 3 – x
a) x = – 3 có thỏa mãn phương trình không ?
b) x = 0 có là một nghiệm của phương trình không?
Hướng dẫn:
a) 2(x + 3) – 3 = 2(– 3 + 3) – 3 = 2. 0 – 3 = 0 – 3 = – 3
Ta có: 3 – x = 3 – (– 3) = 6 ≠ – 3
Vậy x = – 3 không thỏa mãn phương trình
b) 2(0 + 3) – 3 = 2.3 – 3 = 6 – 3 = 3
Ta có: 3 – x = 3 – 0 = 3
⇒ x = 0 có là một nghiệm của phương trình
Vậy x = 0 là nghiệm của phương trình.
Bài 4:
a) Tìm giá trị của m sao cho phương trình sau nhận x = 2 làm nghiệm: 3x – 2m = x + 5.
b) Tìm giá trị của m, biết rằng phương trình: nhận x = 2 làm nghiệm: 5m – 7x = 3x
Hướng dẫn:
a) Phương trình 3x – 2m = x + 5 nhận x = 2 làm nghiệm nên ta có:
3.2 – 2m = 2 + 5
⇔ 2m = – 1 ⇔ m = – 1/2
Vậy m = – 1/2
b) Phương trình 5m – 7x = 3x nhận x = 2 làm nghiệm nên ta có:
5m – 7.2 = 3.2 ⇔ 5m = 20 ⇔ m = 4
Vậy m = 4
Bài 5: Giải phương trình:
a) 3x + 1 = x + 2
b) (x – 1)2 = x2 + 6x – 3
c) x2 + 5 = 6x – 4
Hướng dẫn:
a) Phương trình ⇔ 2x – 1 = 0 ⇔ x = 1/2
Vậy phương trình có nghiệm
b) Phương trình ⇔ x2 – 2x + 1 = x2 + 6x – 3
⇔ – 8x + 4 = 0
⇔ x = 1/2
Vậy phương trình có nghiệm x = 1/2
c) Phương trình ⇔ x2 – 6x + 9 = 0
⇔ (x – 3)2 = 0
⇔ x = 3
Vậy phương trình có nghiệm x = 3
Bài 6: Giải phương trình:
a, x(x + 3) = (3 – x)(1 + x)
b, x3 – 4x2 + 5x – 2 = 0
c, (x + 1)2(x + 2) + (x – 1)2(x – 2) = – 12
Hướng dẫn:
a, Phương trình ⇔ x2 + 3x = 3 + 2x – x2
⇔ 2x2 + x – 3 = 0
⇔ (x – 1)(2x + 3) = 0
Vậy tập nghiệm của phương trình là S = { – 3/2;1 }
b, Phương trình ⇔ x3 – 2x2 – 2x2 + 4x + x – 2 = 0
⇔ (x – 2)(x2 – 2x + 1) = 0
⇔ (x – 2)(x – 1)2 = 0
Vậy tập nghiệm của phương trình là S = { 1;2 }
c, Phương trình ⇔ 2x3 + 10x = – 12 ⇔ x3 + 5x + 6 = 0
⇔ (x3 + 1) + 5(x + 1) = 0 ⇔ (x + 1)(x2 – x + 6) = 0
⇔ x = – 1 ⇔ x + 1 = 0 (Do x2 – x + 6 = (x – 1/2)2 + 23/4 > 0 ∀ x )
Vậy phương trình có nghiệm x = – 1
Bài 7: Giải các phương trình sau
Hướng dẫn:
a, Ta có:
⇔ 5x + 1 = – 15 ⇔ x = – 16/5
Vậy tập nghiệm của phương trình là S = { – 16/5 }
b, Ta có:
⇔ 25x + 20 = 18x + 12 ⇔ x = – 8/7
Vậy tập nghiệm của phương trình là S = { – 8/7 }
Bài 8: Giải phương trình:
Hướng dẫn:
ĐKXĐ: x ≠ ± 1;x ≠ ± 2
Phương trình
⇔ 6x2 – 12 = 0 ⇔ x = ± √ 2 (TMĐK)
Vậy tập nghiệm của phương trình là S = { ± √ 2 }
Bài 9: Mẫu số của một phân số lớn hơn tử của nó là 5 đơn vị, nếu tăng cả tử thêm 2 đơn vị và mẫu thêm 4 đơn vị, thì được một phân số mới bằng phân số ban đầu . Tìm phân số cho ban đầu
Hướng dẫn:
Gọi tử số của phân số ban đầu là a, theo bài ra ta có:
(Điều kiện: a ≠ – 5;a ≠ – 9 )
⇔ a2 + 9a = a2 + 7a + 10
⇔ 2a = 10 ⇔ a = 5 (Thỏa mãn)
Vậy phân số cần tìm là: 5/10
Bài 10: Giải phương trình:
a, 2(x + 1)(8x + 7)2(4x + 3) = 9
b, (x2 – 4)2 = 8x + 1
Hướng dẫn:
a, Phương trình ⇔ (8x + 8)(8x + 7)2(8x + 6) = 72
Đặt 8x + 7 = t, phương trình trở thành: (t + 1)t2(t – 1) = 72
⇔ t2(t2 – 1) – 72 = 0 ⇔
Với t = 3 ⇒ x = – 1/2
Với t = – 3 ⇒ x = – 5/4
Vậy tập nghiệm của phương trình là S = { – 1/2; – 5/4 }
b, Phương trình ⇔ (x2 – 4)2 + 16x2 = 16x2 + 8x + 1
⇔ (x2 + 4)2 = (4x + 1)2 ⇔
⇔ x2 – 4x + 3 = 0 (Do x2 + 4x + 5 = (x + 2)2 + 1 > 0 ∀ x )
Vậy tập nghiệm của phương trình là S = { 1;3 }
2. Vận dụng – Vận dụng cao
Bài 1: Giải phương trình:
a, x4 + x3 + x2 + x + 1 = 0
b, x5 = x4 + x3 + x2 + x + 2
Hướng dẫn:
a, Ta thấy x = 1 không phải nghiệm của phương trình nên nhân 2 vế của phương trình với x – 1 ta có: (x – 1)(x4 + x3 + x2 + x + 1) = 0
⇔ x5 – 1 = 0
⇔ x = 1(KTM)
Vậy phương trình đã cho vô nghiệm.
b, Phương trình ⇔ x5 – 1 = x4 + x3 + x2 + x + 1
⇔ (x – 1)(x4 + x3 + x2 + x + 1) = x4 + x3 + x2 + x + 1
⇔ (x – 2)(x4 + x3 + x2 + x + 1) = 0
⇔ x = 2 (Vì theo phần a)
Vậy phương trình có nghiệm duy nhất x = 2
Bài 2: Giải các phương trình sau
a)
b)
Hướng dẫn:
a) Ta có: Phương trình
⇔ x – 2020 = 0
⇔ x = 2020
Vậy phương trình có nghiệm là x = 2020
b) Ta có:
⇔ x – 64 = 0 ⇔ x = 64
Vậy phương trình đã cho có nghiệm là x = 64
Bài 3: Giải phương trình
Hướng dẫn:
a, ĐKXĐ: x ≠ 1;x ≠ 2;x ≠ 3;x ≠ 4
Phương trình
Vậy tập nghiệm của phương trình là S = { 0;5/2 }
b, ĐKXĐ: x3 – x2 – x ≠ 0 ⇔ x( x2 – x – 1 ) ≠ 0
Phương trình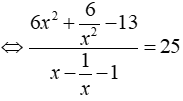
Đặt x – 1/x = t ⇒ t2 = x2 + 1/x2 – 2
Phương trình trở thành:
⇔ 6t2 – 25t + 24 = 0
⇔ (3t – 8)(2t – 3) = 0
Với t = 8/3 ta có: ⇒ 3x2 – 8x – 3 = 0 ⇔ (3x + 1)(x – 3) = 0
Làm tương tự với t = 3/2 ta có:
Vậy tập nghiệm của phương trình là S = { – 1/2; – 1/3;2;3 }
c, ĐKXĐ: x ∉ 2;3;4;5;6
Phương trình
⇔ (x – 6)(x – 2) = 12
⇔ x(x – 8) = 0 ⇔
Vậy phương trình đã cho có tập nghiệm là S = { 0;8 }
Bài 4: Giải phương trình:
a) (x2 – 1)(x2 + 4x + 3) = – 3
b) (x + 4)3 – (x + 2)3 = 56
c) (x + 1)4 + (x + 3)4 = 16
Hướng dẫn:
a, Phương trình ⇔ (x – 1)(x + 1)(x + 1)(x + 3) = – 3
⇔ (x2 + 2x – 3)(x2 + 2x + 1) + 3 = 0
Đặt x2 + 2x – 1 = t khi đó phương trình trở thanh: (t – 2)(t + 2) + 3 = 0
⇔ t2 – 1 = 0 ⇔
Với t = 1 ta có: x2 + 2x – 1 = 1 ⇔ (x + 1)2 – 3 = 0 ⇔ x = – 1 ± √ 3
Với t = – 1 ta có: x2 + 2x – 1 = – 1 ⇔ x(x + 2) = 0
Vậy tập nghiêm của phương trình là S = { – 2;0; – 1 ± √ 3 }
b, Phương trình ⇔ 2(x2 + 8x + 16 + x2 + 6x + 8 + x2 + 4x + 4) = 56
⇔ 3x2 + 18x = 0
Vậy tập nghiệm của phương trình là S = { – 18/3;0 }
`
c, Đặt x + 2 = t, phương trình trở thành: (t – 1)4 + (t + 1)4 = 16
⇔ 2t4 + 12t2 + 2 = 16 ⇔ t4 + 6t2 – 7 = 0
Với t2 = 1 ta có: (x + 2)2 = 1
Vậy tập nghiệm của phương trình là S = { – 3; – 1 }
Bài 5: Ông A có 1 số tiền tiết kiệm. Biết rằng trong 1 năm ông ta đều tiêu 100 đô và tăng thêm một phần tư số tiền còn lại. Sau 3 năm thì ông ta có gấp rưỡi số tiền tiết kiệm ban đầu. Tính số tiền tiết kiệm ban đầu của ông A.
Hướng dẫn:
Gọi số tiền tiết kiệm lúc đầu của ông A là x
Sô tiền của ông A sau năm đầu tiên là:
Số tiền của ông A sau năm hai là:
Số tiền của ông A sau năm ba là:
Theo bài ra ta có:
Vậy số tiền tiết kiệm lúc đầu của ông A là: 30500/29 (Đô)
Thông báo: Blog Lương Điệp (luongdiep.com) là nơi chia sẻ Template Powerpoint; Trò chơi Powerpoint; Tài liệu Giáo dục; Bài giảng điện tử; Giáo án điện tử; Đề thi: học tập trực tuyến, ... miễn phí, phi lợi nhuận.
Nếu bạn sở hữu file do bản quyền thuộc về bạn, hãy liên hệ ngay với chúng tôi để chúng tôi tháo gỡ theo yêu cầu. Xin cám ơn!