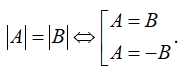I. CĂN THỨC BẬC HAI
1. Định nghĩa
Với A là một biểu thức đại số, người ta gọi √A là căn thức bậc hai của A, còn A là biểu thức lấy căn hay còn gọi là biểu thức dưới dấu căn.
2. Điều kiện có nghĩa(hay có nghĩa) của một căn thức bậc hai
√A xác định(có nghĩa) ⇔ A ≥ 0
3. Ví dụ cụ thể
– 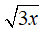
– 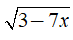
– 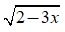
– 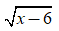
– 
II. HẰNG ĐẲNG THỨC
Muốn khai căn một biểu thức, ta dùng hằng đẳng thức √(A2) = |A|.
Ví dụ 1: Rút gọn biểu thức 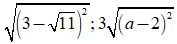
Giải:
Ta có: 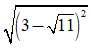
Ta có: 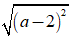
Khi đó: 3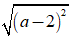
Ví dụ 2: Tìm x biết √(x2) = |-7|; √(9x2) = |-12|
Giải:
Ta có: √(x2) = |-7| = 7 ⇔ x2 = 49 ⇔ x = ±7
Ta có: √(9x2) = |-12| = 12 ⇔ 9x2 = 144 ⇔ x2 = 16 ⇔ x = ±4
III. MỘT SỐ KIẾN THỨC CẦN NHỚ
1. Giá trị tuyệt đối
• Định nghĩa
• Hệ quả
|A| ≥ 0, ∀ A
|A| = |-A|
|A| = A ⇔ A ≥ 0; |A| = -A ⇔ A ≤ 0; |A| = 0 ⇔ A = 0
2. Dấu của một tích, một thương
B. PHƯƠNG PHÁP GIẢI TOÁN
DẠNG 1: Tìm điều kiện để một để một căn thức bậc hai xác định.
• √A xác định (hay có nghĩa) ⇔ A ≥ 0
• Giải bất phương trình A ≥ 0
• Kết luận.
DẠNG 2: Khai căn một biểu thức – Tính giá trị một biểu thức chứa căn
• Khai căn nhờ hằng đẳng thức √(A2) = |A|
• Rút gọn
DẠNG 3: Phân tích thành nhân tử
• Viết A ≥ 0 thành (√A)2
• Sử dụng A2 – B2 = (A – B)(A + B)
• Sử dụng A2 ± 2AB + B2 = (A ± B)2
• Thêm, bớt tạo thành hằng đẳng thức
DẠNG 4: Giải phương trình
• Khai căn một biểu thức
• Giải phương trình chứa dấu giá trị tuyệt đối
Thông báo: Blog Lương Điệp (luongdiep.com) là nơi chia sẻ Template Powerpoint; Trò chơi Powerpoint; Tài liệu Giáo dục; Bài giảng điện tử; Giáo án điện tử; Đề thi: học tập trực tuyến, ... miễn phí, phi lợi nhuận.
Nếu bạn sở hữu file do bản quyền thuộc về bạn, hãy liên hệ ngay với chúng tôi để chúng tôi tháo gỡ theo yêu cầu. Xin cám ơn!