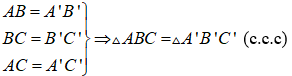Bài 3: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (c.c.c)

A. Lý thuyết

1. Vẽ tam giác biết ba cạnh

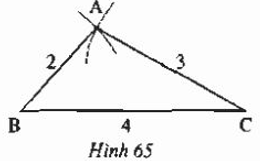
Bài toán: Vẽ tam giác ABC, biết AB = 2cm, BC = 4cm, AC = 3cm

• Vẽ đoạn thẳng BC = 4cm.

• Trên cùng một nửa mặt phẳng bờ BC, vẽ cung tròn tâm B bán kính 2cm và cung tròn tâm c bán kính 3cm.

• Hai cung tròn trên cắt nhau tại A.

• Vẽ các đoạn thẳng AB, AC, ta được tam giác ABC.

2. Trường hợp bằng nhau cạnh – cạnh – cạnh

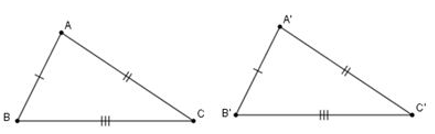
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau theo trường hợp cạnh – cạnh – cạnh.

ΔABC và ΔA’B’C’ có:

B. Bài tập

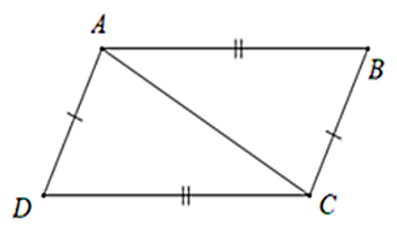
Bài 1: Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán bính BA, chúng cách nhau giữa ở D (D và B nằm khác phía đối với bờ AC). Chứng minh rằng AD // BC

Hướng dẫn giải:

Xét ΔABC và ΔCDA có AC chung

AB = CD (gt)

BC = DA (gt)

Nên ΔABC = ΔCDA (c-c-c)

⇒ ∠ABC = ∠CAD (hai góc tương ứng bằng nhau)

Hai đường thẳng AD, BC tạo AC hai góc so le

Do đó AD // BC

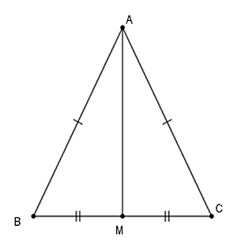
Bài 2: Tam giác ABC có AB = AC, M là trung điểm của BC. Chứng mình rằng AM vuông góc với BC.

Hướng dẫn giải:

Xét ΔAMB và ΔAMC có:

AB = AC

AM chung

MB = MC (gt)

⇒ ΔAMB = ΔAMC (c-c-c)

Suy ra ∠BAM = ∠CAM; ∠AMB = ∠AMC (góc tương ứng bằng nhau)

Mà ∠AMB + ∠AMC = 180° (hai góc kề bù)

Nên ∠AMB = ∠AMC = 180°/2 = 90° hay AM ⊥ BC