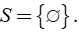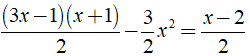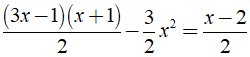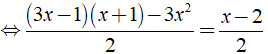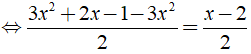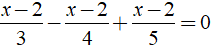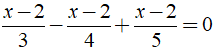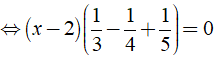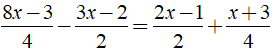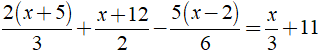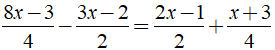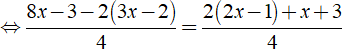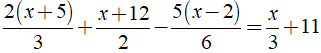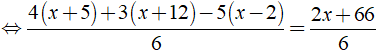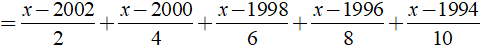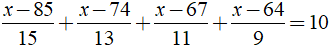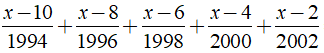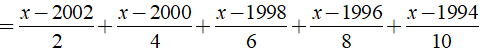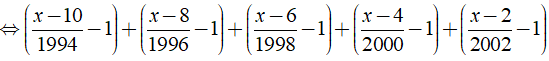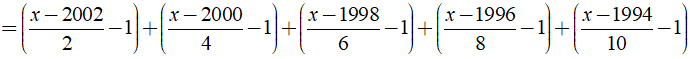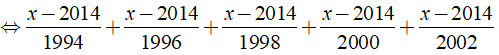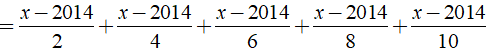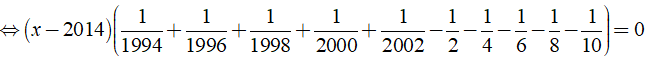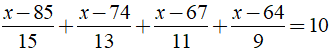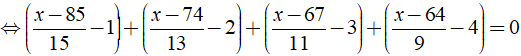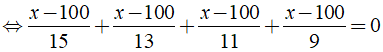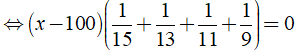Bài 3: Phương trình đưa được về dạng ax + b = 0 – Luyện tập

1. Cách giải

Để giải các phương trình đưa được về ax + b = 0 ta thường biến đổi phương trình như sau:

Bước 1: Quy đồng mẫu hai vế và khử mẫu (nếu có)

Bước 2: Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax = c.

Bước 3: Tìm x

Chú ý: Quá trình biến đổi phương trình về dạng ax = c có thể dẫn đến trường hợp đặc biệt là hệ số của ẩn bằng 0 nếu:

0x = c thì phương trình vô nghiệm

0x = 0 thì phương trình nghiệm đúng với mọi x hay vô số nghiệm S = R.

Ví dụ 1: Giải phương trình 2x – ( 3 – 2x ) = 3x + 1

Hướng dẫn:

Ta có 2x – ( 3 – 2x ) = 3x + 1 ⇔ 2x – 3 + 2x = 3x + 1

⇔ 4x – 3x = 1 + 3 ⇔ x = 4.

Vậy phương trình đã cho có tập nghiệm là S = { 4 }.

Ví dụ 2: Giải phương trình

Hướng dẫn:

Ta có:

⇔ 2x – 1 = x – 2 ⇔ x = – 1.

Vậy phương trình đã cho có tập nghiệm là S = { – 1 }.

Ví dụ 3: Giải phương trình

Hướng dẫn:

Ta có:

⇔ ( x – 2 )17/60 = 0 ⇔ x – 2 = 0 ⇔ x = 2.

Vậy phương trình có tập nghiệm là S = { 2 }.

Ví dụ 4: Giải phương trình x + 1 = x – 1.

Hướng dẫn:

Ta có x + 1 = x – 1 ⇔ x – x = – 1 – 1 ⇔ 0x = – 2.

Vậy phương trình đã cho vô nghiệm.

Ví dụ 5: Giải phương trình x – 3 = x – 3.

Hướng dẫn:

Ta có: x – 3 = x – 3 ⇔ x – x = – 3 + 3 ⇔ 0x = 0.

Vậy phương trình đã cho vô số nghiệm.

* Bài tập:

Bài 1: Giải các phương trình sau:

a) 5( x – 3 ) – 4 = 2( x – 1 ) + 7

b)

c)

Hướng dẫn:

a) Ta có: 5( x – 3 ) – 4 = 2( x – 1 ) + 7

⇔ 5x – 15 – 4 = 2x – 2 + 7

⇔ 5x – 2x = 15 + 4 + 2 – 7

⇔ 3x = 14 ⇔ x = 14/3

Vậy phương trình đã cho có nghiệm là x = 14/3.

b) Ta có:

⇔ 8x – 3 – 6x + 4 = 4x – 2 + x + 3

⇔ 5x – 2x = 6 – 6 ⇔ x = 0

Vậy phương trình đã cho có nghiệm là x = 0.

c) Ta có:

⇔ 4x + 20 + 3x + 36 – 5x + 10 = 2x + 66

⇔ 0x = 0

⇒ Phương trình đã cho vô số nghiệm.

Vậy phương trình đã cho vô số nghiệm.

Bài 2: Giải các phương trình sau

a)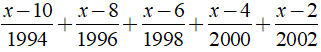 

b)

Hướng dẫn:

a) Ta có:

⇒ x – 2014 = 0 ⇔ x = 2014.

Vậy phương trình đã cho có nghiệm là x = 2014.

b) Ta có:

⇒ x – 100 = 0 ⇔ x = 100.

Vậy phương trình đã cho có nghiệm là x = 100.